Evaluation

cross_validation(
    n_folds::Integer,
    metric::Union{RankingMetric, AggregatedMetric, Coverage, Novelty},
    topk::Integer,
    recommender_type::Type{<:Recommender},
    data::DataAccessor,
    recommender_args...;
    allow_repeat::Bool=false
)

Conduct n_folds cross validation for a combination of recommender recommender_type and ranking metric metric. A recommender is initialized with recommender_args and runs top-k recommendation.

cross_validation(
    n_folds::Integer,
    metric::AccuracyMetric,
    recommender_type::Type{<:Recommender},
    data::DataAccessor,
    recommender_args...
)

Conduct n_folds cross validation for a combination of recommender recommender_type and accuracy metric metric. A recommender is initialized with recommender_args.

leave_one_out(
    metric::RankingMetric,
    topk::Integer,
    recommender_type::Type{<:Recommender},
    data::DataAccessor,
    recommender_args...
)

Conduct leave-one-out cross validation (LOOCV) for a combination of recommender recommender_type and accuracy metric metric. A recommender is initialized with recommender_args and runs top-k recommendation.

leave_one_out(
    metric::AccuracyMetric,
    recommender_type::Type{<:Recommender},
    data::DataAccessor,
    recommender_args...
)

Conduct leave-one-out cross validation (LOOCV) for a combination of recommender recommender_type and accuracy metric metric. A recommender is initialized with recommender_args.

RMSE

Root Mean Squared Error.

measure(
    metric::RMSE,
    truth::AbstractVector,
    pred::AbstractVector
)

truth and pred are expected to be the same size.

MAE

Mean Absolute Error.

measure(
    metric::MAE,
    truth::AbstractVector,
    pred::AbstractVector
)

truth and pred are expected to be the same size.

Recall

Recall-at-$k$ (Recall@$k$) indicates coverage of truth samples as a result of top-$k$ (topk) recommendation. The value is computed by the following equation:

\[\mathrm{Recall@}k = \frac{|\mathcal{I}^+_u \cap I_N(u)|}{|\mathcal{I}^+_u|}.\]

Here, $|\mathcal{I}^+_u \cap I_N(u)|$ is the number of true positives.

measure(
    metric::Recall,
    truth::AbstractVector{T},
    pred::AbstractVector{T},
    topk::Integer
)

Precision

Precision-at-$k$ (Precision@$k$) evaluates correctness of a top-$k$ (topk) recommendation list $I_N(u)$ according to the portion of true positives in the list as:

\[\mathrm{Precision@}k = \frac{|\mathcal{I}^+_u \cap I_N(u)|}{|I_N(u)|}.\]

measure(
    metric::Precision,
    truth::AbstractVector{T},
    pred::AbstractVector{T},
    topk::Integer
)

MAP

While the original Precision@$N$ provides a score for a fixed-length recommendation list $I_N(u)$, mean average precision (MAP) computes an average of the scores over all recommendation sizes from 1 to $|\mathcal{I}|$. MAP is formulated with an indicator function for $i_n$, the $n$-th item of $I(u)$, as:

\[\mathrm{MAP} = \frac{1}{|\mathcal{I}^+_u|} \sum_{n = 1}^{|\mathcal{I}|} \mathrm{Precision@}n \cdot \mathbb{1}_{\mathcal{I}^+_u}(i_n).\]

It should be noticed that, MAP is not a simple mean of sum of Precision@$1$, Precision@$2$, $\dots$, Precision@$|\mathcal{I}|$, and higher-ranked true positives lead better MAP.

measure(
    metric::MAP,
    truth::AbstractVector{T},
    pred::AbstractVector{T}
)

AUC

ROC curve and area under the ROC curve (AUC) are generally used in evaluation of the classification problems, but these concepts can also be interpreted in a context of ranking problem. Basically, the AUC metric for ranking considers all possible pairs of truth and other items which are respectively denoted by $i^+ \in \mathcal{I}^+_u$ and $i^- \in \mathcal{I}^-_u$, and it expects that the $best'' recommender completely ranks$i^+$higher than$i^-``, as follows:

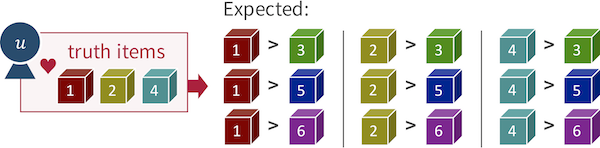
AUC calculation keeps track the number of true positives at different rank in $\mathcal{I}$. At line 8, the function adds the number of true positives which were ranked higher than the current non-truth sample to the accumulated count of correct pairs. Ultimately, an AUC score is computed as portion of the correct ordered $(i^+, i^-)$ pairs in the all possible combinations determined by $|\mathcal{I}^+_u| \times |\mathcal{I}^-_u|$ in set notation.

measure(
    metric::AUC,
    truth::AbstractVector{T},
    pred::AbstractVector{T}
)

ReciprocalRank

If we are only interested in the first true positive, reciprocal rank (RR) could be a reasonable choice to quantitatively assess the recommendation lists. For $n_{\mathrm{tp}} \in \left[ 1, |\mathcal{I}| \right]$, a position of the first true positive in $I(u)$, RR simply returns its inverse:

\[ \mathrm{RR} = \frac{1}{n_{\mathrm{tp}}}.\]

RR can be zero if and only if $\mathcal{I}^+_u$ is empty.

measure(
    metric::ReciprocalRank,
    truth::AbstractVector{T},
    pred::AbstractVector{T}
)

MPR

Mean percentile rank (MPR) is a ranking metric based on $r_{i} \in [0, 100]$, the percentile-ranking of an item $i$ within the sorted list of all items for a user $u$. It can be formulated as:

\[\mathrm{MPR} = \frac{1}{|\mathcal{I}^+_u|} \sum_{i \in \mathcal{I}^+_u} r_{i}.\]

$r_{i} = 0\%$ is the best value that means the truth item $i$ is ranked at the highest position in a recommendation list. On the other hand, $r_{i} = 100\%$ is the worst case that the item $i$ is at the lowest rank.

MPR internally considers not only top-$N$ recommended items also all of the non-recommended items, and it accumulates the percentile ranks for all true positives unlike MRR. So, the measure is suitable to estimate users' overall satisfaction for a recommender. Intuitively, $\mathrm{MPR} > 50\%$ should be worse than random ranking from a users' point of view.

measure(
    metric::MPR,
    truth::AbstractVector{T},
    pred::AbstractVector{T}
)

NDCG

Like MPR, normalized discounted cumulative gain (NDCG) computes a score for $I(u)$ which places emphasis on higher-ranked true positives. In addition to being a more well-formulated measure, the difference between NDCG and MPR is that NDCG allows us to specify an expected ranking within $\mathcal{I}^+_u$; that is, the metric can incorporate $\mathrm{rel}_n$, a relevance score which suggests how likely the $n$-th sample is to be ranked at the top of a recommendation list, and it directly corresponds to an expected ranking of the truth samples.

measure(
    metric::NDCG,
    truth::AbstractVector{T},
    pred::AbstractVector{T},
    topk::Integer
)

AggregatedDiversity

The number of distinct items recommended across all suers. Larger value indicates more diverse recommendation result overall.

measure(
    metric::AggregatedDiversity, recommendations::AbstractVector{<:AbstractVector{<:Integer}}
)

Let $U$ and $I$ be a set of users and items, respectively, and $L_N(u)$ a list of top-$N$ recommended items for a user $u$. Here, an aggregated diversity can be calculated as:

\[\left| \bigcup\limits_{u \in U} L_N(u) \right|\]

ShannonEntropy

If we focus more on individual items and how many users are recommended a particular item, the diversity of topk recommender can be defined by Shannon Entropy:

\[-\sum_{j = 1}^{|I|} \left( \frac{\left|\{u \mid u \in U \wedge i_j \in L_N(u) \}\right|}{N |U|} \ln \left( \frac{\left|\{u \mid u \in U \wedge i_j \in L_N(u) \}\right|}{N |U|} \right) \right)\]

where $i_j$ denotes $j$-th item in the available item set $I$.

measure(
    metric::ShannonEntropy, recommendations::AbstractVector{<:AbstractVector{<:Integer}};
    topk::Integer
)

GiniIndex

Gini Index, which is normally used to measure a degree of inequality in a distribution of income, can be applied to assess diversity in the context of topk recommendation:

\[\frac{1}{|I| - 1} \sum_{j = 1}^{|I|} \left( (2j - |I| - 1) \cdot \frac{\left|\{u \mid u \in U \wedge i_j \in L_N(u) \}\right|}{N |U|} \right)\]

measure(
    metric::GiniIndex, recommendations::AbstractVector{<:AbstractVector{<:Integer}};
    topk::Integer
)

The index is 0 when all items are equally chosen in terms of the number of recommended users.

Coverage

Catalog coverage is a ratio of recommended items among catalog, which represents a set of all available items.

measure(
    metric::Coverage, recommendations::Union{AbstractSet, AbstractVector};
    catalog::Union{AbstractSet, AbstractVector}
)

Novelty

The number of recommended items that have not been observed yet i.e., not in observed.

measure(
    metric::Novelty, recommendations::Union{AbstractSet, AbstractVector};
    observed::Union{AbstractSet, AbstractVector}
)

IntraListSimilarity

Sum of similarities between every pairs of recommended items. Larger value represents less diversity.

• Reference: Improving Recommendation Lists Through Topic Diversification

measure(
    metric::IntraListSimilarity, recommendations::Union{AbstractSet, AbstractVector};
    sims::AbstractMatrix
)

Serendipity

Return a sum of relevance-unexpectedness multiplications for all recommended items.

measure(
    metric::Serendipity, recommendations::Union{AbstractSet, AbstractVector};
    relevance::AbstractVector, unexpectedness::AbstractVector
)